時間に依る摂動論; S行列

Prerequisite

散乱理論における摂動論
定常散乱のS行列

前節までの散乱状態に関する結果を別な形にまとめていこう．
散乱理論は定常な場合，S行列を使って記述できたことを思い起こす．
時間に依存する摂動のうち，ある有限の時間だけ一定の摂動が作用するような時間依存性の場合は，この定常散乱の議論と結びつけることが可能となる．

まず既知のHamiltonianを $\hat{H}_0$ としその固有状態を一般に $|{\alpha;0}\rangle$ とし，正規直交完全系をなすとする:

$\widetilde{\mathrm{d}\alpha}$ は適当な測度（たとえば運動量の場合は $\widetilde{\mathrm{d}\boldsymbol{p}}=\mathrm{d}^3\boldsymbol{p}/(2\pi\hbar)^3$ ）．
前節までは運動量の固有状態だったが，スピンや他の物理量を含めてもよい．
セミコロンの後の $0$ はこれまで同様に摂動のないときの固有状態を意味する．
任意の時刻 $t$ における波束状態は

として構成できる．
$a(t,\alpha)$ はある $\alpha=\alpha_*$ にピークを持って局在化した函数．
ある基準となる時刻 $t=t_0$ を決めると摂動がないときの時間発展演算子を用いて

と書ける．
ここまでは摂動のないときの系に関する準備である．

では次に摂動がある場合の準備をしていこう．
摂動を $\hat{H}_{1}(t)$ とし有限時間 $[-T,\,T]$ の間だけ定常な摂動 $\lambda\hat{V}$ を印加するものとする:

$\lambda$ は摂動の微小パラメータ．
全Hamiltonian $\,\hat{H}=\hat{H}_0+\lambda\hat{V}$ の固有状態を添字 $0$ のない $|{\alpha}\rangle$ として

が成り立つとする．
摂動があるときには相互作用描像をとって任意の状態ベクトルは

と時間発展する．
他方でSchrödinger描像の状態ベクトルと $|{\psi_{\mathrm{I}},t}\rangle=\hat{U}_0^{\dagger}(t-t_0)|{\psi,t}\rangle$ の関係にあるので

$t=t_0$ では2つの描像の状態ベクトルは一致するので，相互作用描像の時間発展演算子 $\hat{U}_{\mathrm{I}}(t,t_0)$ はSchrödinger描像の時間発展演算子 $\hat{U}(t,t_0)$ と

という関係にある（これは一般に2つの描像の演算子 $\hat{O}_{\mathrm{S}}$ と $\hat{O}_{\mathrm{I}}$ の間に成り立つ関係式と異なることに注意せよ）．

$|{\alpha}\rangle$ と $|{\alpha;0}\rangle$ に関する固有値方程式からは物理量 $\alpha$ で表示したLippmann–Schwinger方程式

Lippmann–Schwinger方程式

が導かれる．
上付き添字 $(\pm)$ は $i\epsilon$ 処方の符号をどちらに選んだかに対応する．
また $\mathcal{N}$ の因子は測度 $\widetilde{\mathrm{d}\alpha}$ における $|{\alpha;0}\rangle$ の規格化因子である．
このLippmann–Schwinger方程式は時刻 $t\in[-T,T]$ において成立する．
ある時刻 $t_0\in[-T,T]$ における状態ベクトル $|{\psi_0}\rangle=|{\psi, t_0}\rangle$ は摂動があるときの固有状態 $|{\alpha}\rangle$ で展開される:

摂動が印加される境界の時刻 $t=-T$ と $t=T$ での（相互作用描像の）状態ベクトルはそれぞれ

と書ける．
これらの状態が $T\to\infty$ の極限では摂動がないときの固有状態 $|{\alpha;0}\rangle$ で記述される系に漸近すると仮定してin状態とout状態を

と定義する（Schrödinger描像に戻せば前節での定義と一致することがわかる）．

定常散乱理論の漸近形の議論から外向き球面波 $|{\alpha^{(+)}\rangle}$ を採用しよう．
in状態とout状態の係数 $a_{\mathrm{in}}(\alpha),\,a_{\mathrm{out}}(\alpha)$ を求めるために左から $\langle{\alpha';0}|$ を作用させると

よって $\langle{\alpha'; 0|\hat{U}_{\mathrm{I}}(\mp T,t_0)|\alpha^{(+)}}\rangle$ に対する $T\to\infty$ の極限を調べれば良い．
まず相互作用描像の時間発展演算子の式により

最後の因子 $\langle{\alpha'; 0|\alpha^{(+)}\rangle}$ はLippmann–Schwinger方程式によって

右辺の第2項の $E_{\alpha}-E_{\alpha'}$ に依存する部分に着目する:

函数 $f_{\mp}(x)$ の $T\to\infty$ でのふるまいを調べたい．
なめらかな函数 $g(x)$ との積の全空間の積分を考えるとデルタ函数の公式により

第1項で変数変換 $\xi=x(\mp T-t_0)/\hbar$ を施すと

となるが $T\to\infty$ の極限で函数 $g$ の引数は $0$ となり積分の外に出せる．
残りの積分 $\mathsf{P}\int\mathrm{d}\xi e^{-i\xi}/\xi$ は複素積分の計算により $-\pi i$ に等しいことがわかる．
よって

すなわち超函数の等号として

が成り立つ．
したがって $T\to\infty$ の極限では

ここで $S_{\alpha'\,\alpha}$ は定常散乱のS行列であり，対応する演算子を $\hat{S}$ として

S行列

で定義される．
S行列を用いてin状態とout状態の展開係数は

となるのでin状態とout状態は

と書ける．
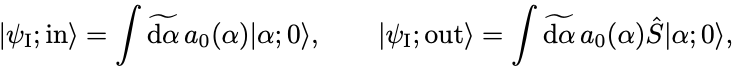
$a_0(\alpha)$ は $\alpha=\alpha_*$ に局在した函数なのでin状態もout状態も波束である．
またin状態とout状態の間には極めてシンプルな関係式

が成り立つことがわかる（こちらをS行列の定義とする場合もある）．
out状態はin状態を用いて相互作用描像の時間発展演算子を用いて

とも書くことができる．
それゆえS行列は $\hat{U}_{\mathrm{I}}$ を用いて

と書き表すこともできる．
これは定常散乱理論で $\hat{\Omega}^{(\pm)}$ を用いて表したことと対応する．
この表式から明らかに $\hat{S}$ はユニタリ演算子である．
$\hat{U}_{\mathrm{I}}$ は時間順序積によって具体的に与えられているので，そこからS行列を計算することが可能である．
特にパラメータ $\lambda$ に関する摂動展開を適用して近似的に評価することもできる．

S行列から $\hat{S}=\hat{I}+2i\hat{T}$ によって遷移行列を定義すれば $\hat{T}$ から遷移振幅が計算できる．
そこから単位時間あたりの遷移確率がもとまり，最終的に微分散乱断面積を与えることができる．
この計算については既に述べた通りである．

注意として，ここでは1つだけ非自明な仮定を置いている．
それは摂動があるときの完全系 $|{\alpha}\rangle$ で展開される状態ベクトルを摂動がないときの完全系 $|{\alpha; 0}\rangle$ で展開できるとしたところである．
たとえばCoulombポテンシャルが $\hat{V}$ として付加された場合，連続なスペクトルの下に束縛状態が現れる．
自由な場合の状態空間とこのような束縛状態を含む状態空間の間で完全性がどのように保たれているかが疑問になる．
ここではこれ以上のこの問題には立ち入らず次の事実だけ述べておく:

束縛状態の空間は散乱状態の空間と直交している（直交性）．
無限過去・未来における状態空間と $t_0\in[-T,\,T]$ における状態空間の散乱状態は同型である（漸近的完全性）．

事実1によって任意の散乱状態の展開式には束縛状態の寄与がないことが保証される．
事実2によって任意のin状態，out状態を $t_0\in[-T,\,T]$ の状態 $|{\psi_0}\rangle$ と関係付けることができる．

最後に重要なこととして，この節では摂動展開は一切用いていないことに注意せよ．
この節で述べた散乱状態に関するS行列の議論は $\hat{H}_0$ で記述される自由な理論と散乱ポテンシャルが加わった $\hat{H}=\hat{H}_0+\hat{V}$ の理論の繋がりを明確にしたことで，散乱のある系の厳密な性質を導けることがある．
詳細は場の量子論の章で述べる．