Prerequisite
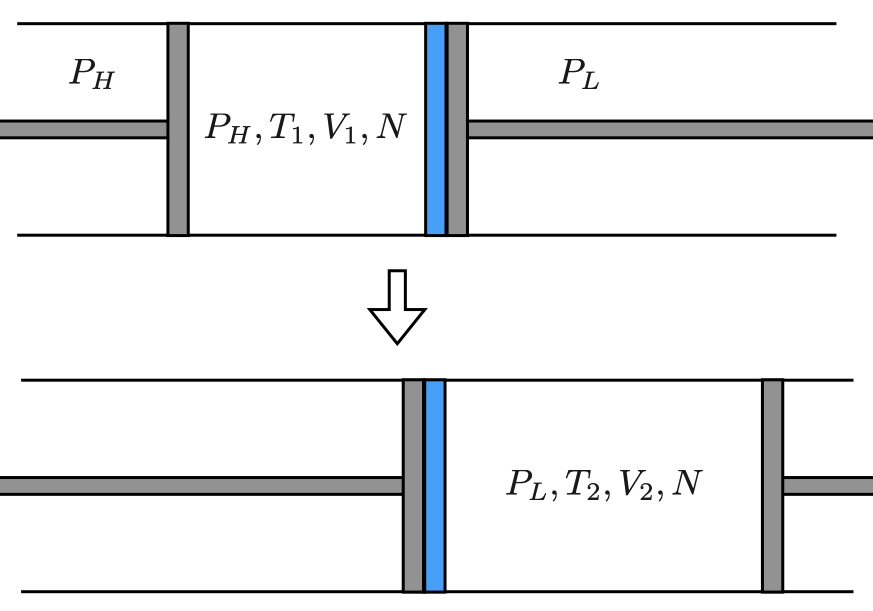
断熱されているが圧力環境 と平衡状態にある部分系1を考える.
この部分系1の温度,体積と粒子数を とする.
部分系1は である低圧力環境
と平衡な部分系2が接触している.
はじめ部分系2には気体はないとし体積も とする.
部分系1と2の間の壁を断熱かつ固定だが粒子を通すものに変える.
ただし粒子の透過がゆっくりになるように透過穴は十分小さいとする.
このとき圧力差によって部分系1の気体は全て部分系2へ押し出されていく.
最終的に部分系1の体積が となり部分系2は
となる.
この過程をJoule–Thomson過程という.
はじめの部分系1の内部エネルギー ,あとの部分系2の内部エネルギーを
とする.
過程はゆっくりなので準静的とみなすと,部分系1には外部圧力により の仕事がなされる.
他方で部分系2は外部に の仕事をなす.
よって熱力学第一法則より

が成立する.
これを整理すると

であるが,これは系のエンタルピー が保存することを示している.
すなわちJoule–Thomson過程は等エンタルピー過程といえる.
この過程での温度変化を評価するために部分系1と2が微小な圧力差 の場合を考える.
微小な圧力差のJoule–Thomson過程での温度変化は

で評価できる. はJoule–Thomson係数と呼ばれる.
たとえば のときJoule–Thomson過程で気体の温度は下がる.
Joule–Thomson係数を実験で計測可能な物理量に書き換えていく.
まずJacobianを用いて
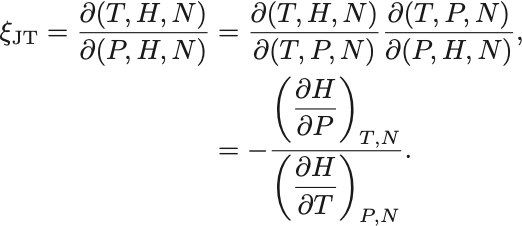
エンタルピーを の函数とみなしときその導函数は
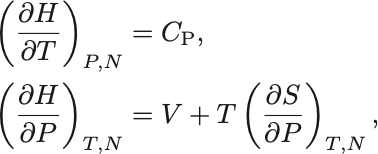
であるから,
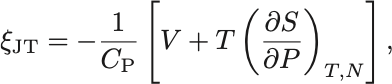
最後にGibbsの自由エネルギーにおけるMaxwellの関係式から
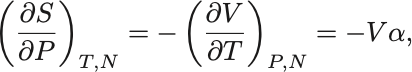
と書き換えられる.
ここで
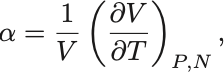
は気体の定圧膨張係数と呼ばれる量である.
以上から
Joule–Thomson係数
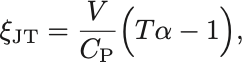
が導かれる.
右辺は全て実験により計測可能な物理量である.
なのでJoule–Thomson係数の符号は
の符号で決まる.
ちょうどこの符号が変わる温度,すなわち
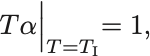
を満たす温度 を逆転温度 (inverse temprature) という.
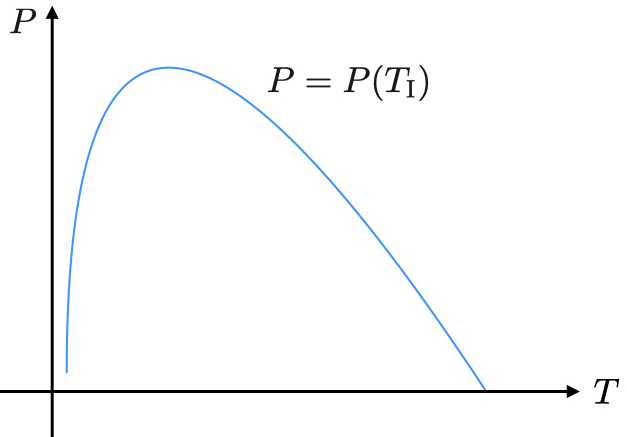
van der Waals気体に対して逆転温度を調べる.
状態方程式
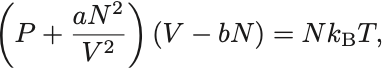
と の条件から
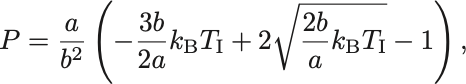
が導かれる.
はじめの圧力を としたときにvan der Waals気体の逆転温度が決まる.
適切な圧力下では低温気体はJoule–Thomson過程でさらに温度が下がる.
このとこを利用し改良を重ねた結果,気体を数Kまで冷却することが可能となり,低温物理学へ多大な影響を与えた.
特にJoule–Thomson過程を応用してH. Kamerlingh Onnesが行ったヘリウムの液体化は超伝導・超流動の発見へとつながったことで物理学史上重要な意味をもつ.
Problems
理想気体のJoule–Thomson係数を求めよ.
ただし理想気体は状態方程式 を満たすとする.
状態方程式を について解いて
を固定して温度で微分すると
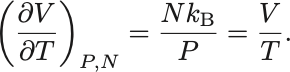
よって定圧膨張係数は
以上から理想気体では常に
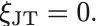
van der Waals気体の圧力から逆転温度を決める式を導出せよ.
状態方程式の両辺を 固定して温度で微分すると

逆転温度においては より

が成立している.
状態方程式を用いて右辺の温度を消去して整理すれば
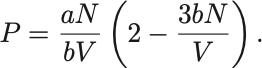
状態方程式にこの式を代入して圧力を消去すれば,

について解くと,
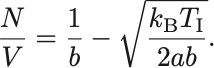
よって圧力の式に現れる をこの式を用いて逆転温度で書き換えれば圧力と逆転温度の関係式を得る.
