Prerequisite
外部との熱などのやりとりが存在しない孤立系においてはエントロピー増大の法則

が成立する.
平衡状態では熱力学変数が一定であることからエントロピーの値は最大であると仮定できる.
言い換えるとエントロピーを記述する示量変数の仮想的な変位に対して必ずエントロピーは強減少する.
これはエントロピー最大の原理である.
孤立系でない他の系でも同様の主張が成立する.
たとえば温度 の熱浴と平衡状態にある系ではHelmholtzの自由エネルギーが最小となることが導かれる.
また温度 かつ圧力
の環境と平衡状態にある系ではGibbsの自由エネルギーが最小となる.
熱浴と平衡状態にある等温過程においてはHelmholtzの自由エネルギーが減少する:

平衡状態では は最小である.
もし平衡状態からわずかにずらす仮想的な変位を考えた場合,Helmholtzの自由エネルギー必ず増加する.
仮想変位によるエントロピーの変位を (体積と粒子数は固定)として内部エネルギーの等温過程での仮想変位を2次まで求めると,
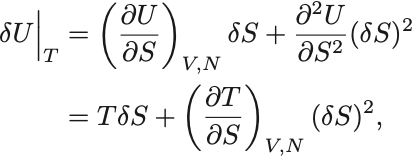
と書ける.
平衡状態の自由エネルギーの最小性からこの仮想変位に対して必ず増加しなければならないから .
内部エネルギーの変位を代入し
熱力学不等式 (1)

が導かれる. であることとJacobianの性質を用いて

が導かれる.
つまり定積比熱は正であることが再導出された.
次にGibbsの自由エネルギー最小の原理について同様の議論をする.
環境と平衡状態にある等温定圧過程においてGibbsの自由エネルギーが減少する:
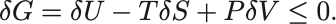
同様に仮想変位 を考え内部エネルギーの変位は
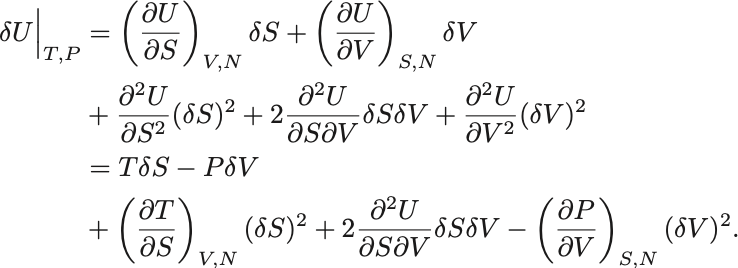
ここで の微分が可換であることに注意せよ.
Gibbsの自由エネルギーの最小性から仮想変位に対して必ず増加するので
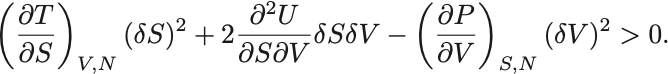
上式を とおいて
について平方完成することで
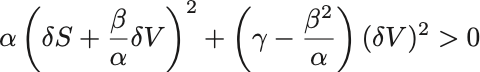
変位は任意であり各2乗の係数が正でなければならないという条件からまず がわかるがこれは定積比熱が正と同じである.
もう一つの係数が正という条件からは

第1項を,

と変形すればJacobianを用いて,

と書き換えられる.
さらにJacobianの性質を用いて
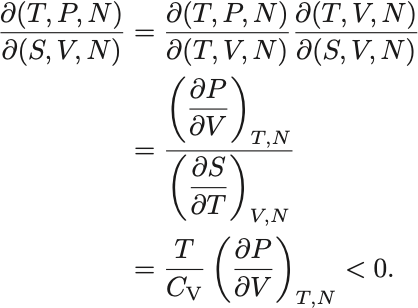
今 であるから,
熱力学不等式 (2)

が導かれる.
この不等式は,等温過程で体積を増大すると圧力が下がることを意味している.
さらに定圧比熱は
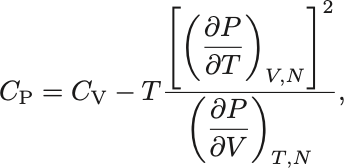
と書けるので
熱力学不等式 (3)

も導かれる.
Next
- 一般の熱力学不等式
