Prerequisite
正準形式の理論を扱う際,一般化座標 の張る空間
上で考えるよりも
と
の張る
上を考える方が便利なことがある.
この空間のことを物理では位相空間 (phase space) といい以下では と書くことにする.
註)数学でいう位相空間 (topological space) とは何の関係もないことに注意.
位相空間 の点は
で表され,正準方程式の解
は位相空間上の一つの曲線軌道に対応する.
そこで座標と運動量をまとめて,
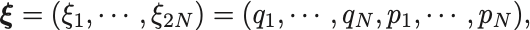
という表記を採用しよう.すると正準方程式は,
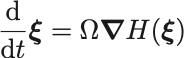
という形にまとめられる.ここで は次の成分をもつ
の正方行列である:

ここで は
次の単位行列.定義から明らかに逆行列は
である.
また微分演算子は,
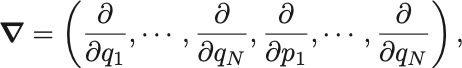
で定義されている.作用は部分積分から,
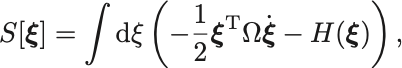
と書き変わる.この作用の に対する変分原理から正準方程式が導かれる.
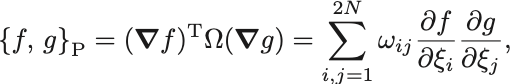
と書き換えることができる.
基本Poisson括弧式と正準方程式は,
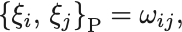

正準変換は位相空間 上の座標変換の1種である.
正準変換を,

とかこう.正準変換の下でPoisson括弧は,
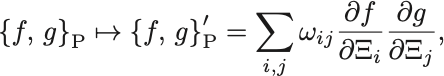
と変換するが,微分の鎖法則より,
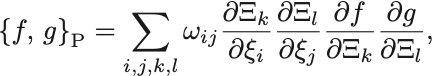
であり,任意の正準変換に対してPoisson括弧の値は不変であることから,
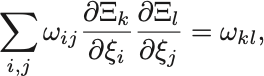
がいえる.
この条件は基本Poisson括弧式が正準変換で不変なことを示しているので, が正準変換であることとこの条件は必要十分の関係にある.
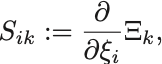
によって行列 を導入しよう.
すると上の条件式は,
シンプレクティック条件
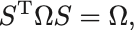
と書き換えられる.
これが位相空間での正準変換の満たすべき条件である.
このような条件を満たす行列 を一般にシンプレクティック行列(symplectic matrix)あるいは斜交行列という.
また は定義より正準変換のJacobi行列でもある.
正準変換を2回続けて行って と変換することを考えよう.それぞれの変換に行列
が対応しているものとする.このとき積
について,
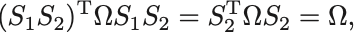
が成り立つので もシンプレクティック行列である.定義より,

となる.つまり合成変換 は正準変換であり対応するシンプレクティック行列は
である.
3つの正準変換に対して行列の積の性質から明らかに結合則 を満たす.
また単位行列 は恒等変換
に対応するシンプレクティック行列である.
任意の正準変換に対して であることから逆行列
が存在する.
そこで の右から
をかけ,左から
をかけると

と表せられる.それゆえ

よって逆行列 もシンプレクティック行列である.
以上のことからシンプレクティック行列全体の集合,
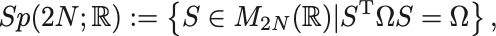
は群構造をもっている.この群をシンプレクティック群あるいは斜交群という.
の左から
をかけると
.
さらに右から をかけると

が得られる.
の両辺の行列式をとれば,
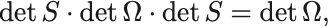
であるので とわかる.
実は であることを示せるがここでは割愛する(問題参照).
Jacobi行列の行列式(Jacobian)が に等しいので位相空間上の積分
は正準変換による変数変換に対して,
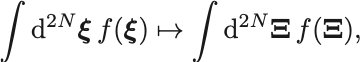
となって積分要素は不変である.この事実をLiouvilleの定理という.
最後に正準方程式の初期値問題の形式解を与えておこう.
正準方程式の両辺をさらに 微分すると
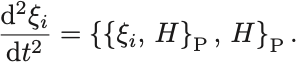
一般に 階微分は

というPoisson括弧が 個入れ子になった形で表すことができる.
正準方程式の初期値を で
として
を初期時刻
の周りでTaylor展開すると
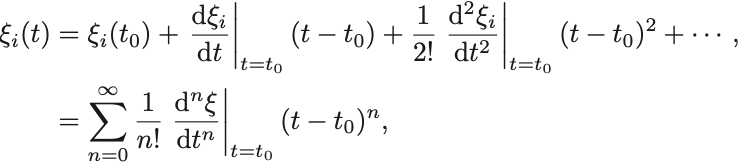
となる. 各項の微分をPoisson括弧で書き換えると
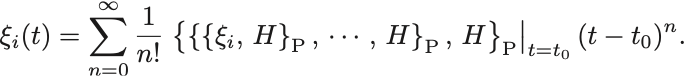
このPoisson括弧の入れ子を微分作用素
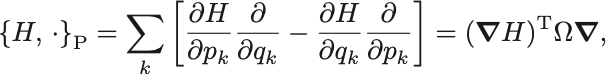
が に
回作用していると解釈すれば
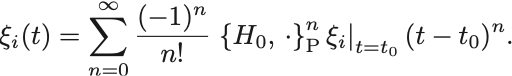
ただし は時刻
でのHamiltonian.
そこで を微分作用素として指数函数
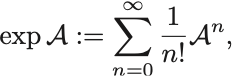
を定義すると,
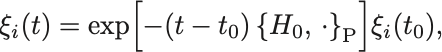
という形の形式解を得ることができる.
正準方程式にしたがう時間発展は1つのパラメータ と生成子
で生成される.
Problems
Lagrange括弧
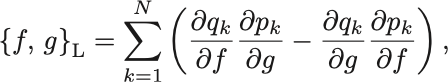
をシンプレクティック表現に改めて,正準変換のもとで不変なことを確かめよ.
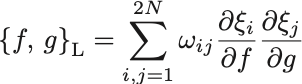
正準変換 に伴って
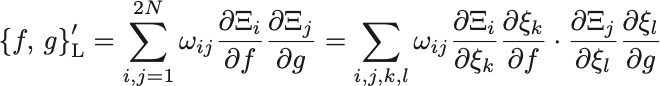
正準変換より なので
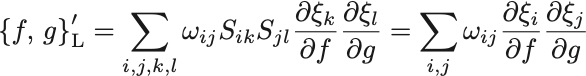
より が示された.
シンプレクティック内積: 位相空間上の任意のベクトル に対してシンプレクティック内積

を定める.シンプレクティック内積が正準変換のもとで不変なことを示せ.
座標基底 をとると,
と展開される.
正準変換 に伴って基底も変換されて
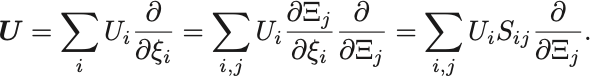
よって正準変換後のベクトルの成分は である.
では正準変換後のシンプレクティック内積は

正準変換ならば なので
.
よって
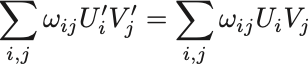
となって不変である.
任意の偶数次の反対称行列 に対して
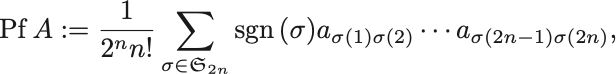
を のPfaffianという.
Pfaffianが任意の行列 と反対称行列
に対して

が成り立つことを用いて,任意のシンプレクティック行列 が
であることを示せ.

シンプレクティック行列より であり,かつ
なので
がしたがう.

“位相空間” への1件のフィードバック