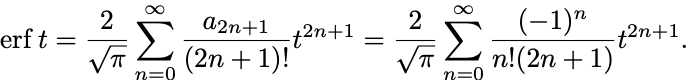Prerequisite
物理学においては,全体の函数形がわからないが限られた領域での振る舞いを議論することがしばしばある.
ある現象を記述する物理量の函数形を初等函数(三角函数や指数・対数函数など)で表せることはまれである.
そこで函数形を厳密に求める代わりに,その振る舞いとよく似た別の初等函数に置き換えることをする.
このとき用いられるテクニックの1つがTaylor展開とよばれるものであり,函数を多項式に置き換えられる.
函数 について
という点をとって

と近似する.
これは でのみ厳密に正しい.
この精度での近似を第0次近似という.
次に の微分に第0次近似を適用して
となるので,両辺を
で積分して戻すと
となる.
で厳密に一致する条件から積分定数は
となって結局,

となる.これは函数を の接線によって近似している.
実際右辺第1項を移項し両辺を で割って
とすればそれは微分の定義になっている.
この精度での近似を一次近似という.
もし何かの議論や計算をしたいときには のままで進めるよりも1次函数の形の方がはるかに容易である.
1次近似では粗すぎると思うときには,第2次近似をとって2階微分 として同様のことを行えばよい.
以下繰り返して,
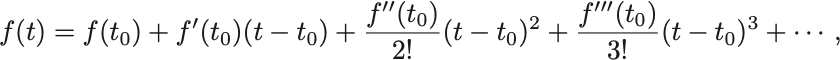
が得ることができる.
これは近似によるナイーブな議論であるから,まずはTaylorの定理を示そう.
Taylorの定理
函数 は
の近傍で
回微分が可能で
は連続とする.
このとき近傍内の任意の においてある
(または
)が存在して,
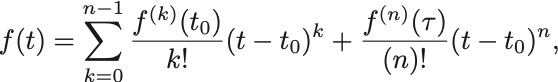
が成立する.
右辺第2項をLagrangeの剰余項という.
証明のために変数 で定義された函数
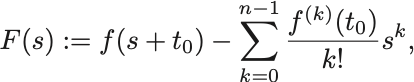
を導入する. としても議論の一般性を失わない.
も
回微分が可能で
かつ
である.
まず と
に対するCauchyの平均値の定理により,
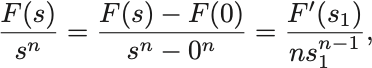
を満たす が存在する.
と
に対するCauchyの平均値の定理により,

を満たす が存在する.
以下これを繰り返して に対して
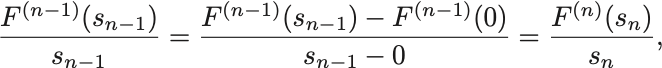
を得る.以上の結果を合わせれば
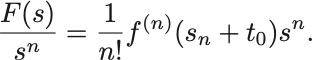
とおいて元の変数
に戻すと,
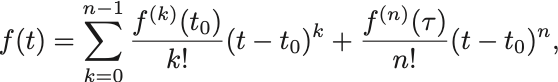
が導かれる .
Taylorの定理の証明には微分の性質しか用いていないことに注意せよ.
Lagrangeの剰余項 とおいたとき,ある
の範囲で
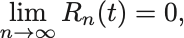
を満たすならば
Taylor展開
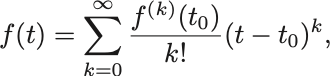
とできる. これを函数 の
まわりのTaylor展開という.
特に のときには,
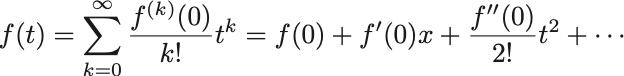
となり,Maclaurin展開とよぶこともある.
本稿では統一してTaylor展開という.
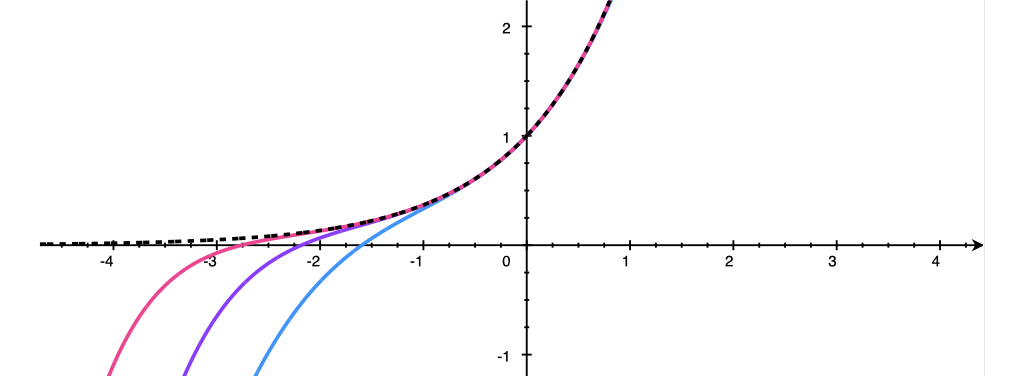
それぞれ3次(青),5次(紫),7次(赤)近似で,高次の項を取り入れるほど元の函数に一致していく.
冒頭で述べたようにTaylor展開が有用であるのはおしなべて函数をその引数の冪で表現できることである.
指数函数のTaylor展開は,

特に のとき
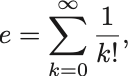
となり,これはNapier数の別表現として知られる.
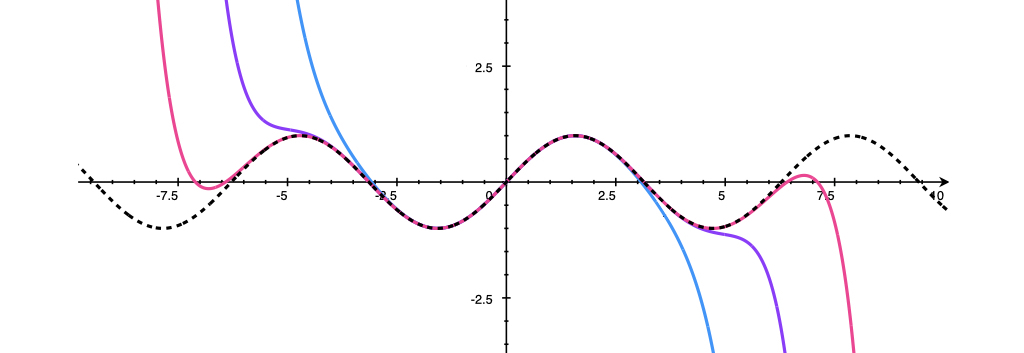
それぞれ3次(青),5次(紫),7次(赤)近似.
三角函数をTaylor展開すれば,
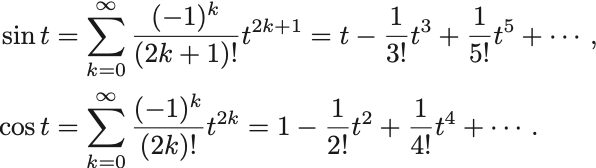
正弦函数は奇数次の項だけが残り,余弦函数では偶数次の項だけが残る.
これは三角函数のグラフの対称性の帰結である.
指数函数も三角函数も全ての で展開可能である.
他に便利な例として
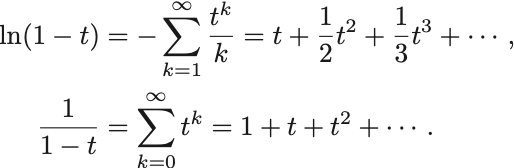
これら2つは でのみ展開可能である.
物理の計算においては厳密な(無限の精度で)値が求まる必要はない.
冪で展開する量 が微小な場合(
)には高次の項は1に比べて十分小さくなるので無視することができる.
よく用いる近似として,2次以上を無視した1次までの近似では,
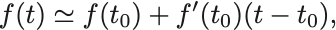
この近似を適用するとたとえば三角函数は のまわりで
,指数函数は
で近似できる.
Problems
次の函数を まわりでTaylor展開せよ:
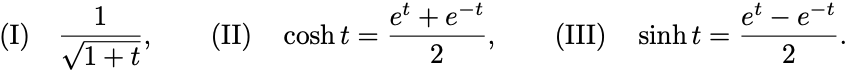
(I) まず3階微分までを計算してみると
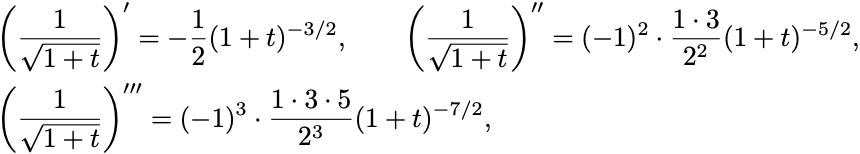
となっている.
ここから 階微分では
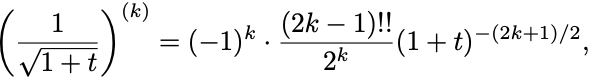
と予想される.
ただし であり
は除外しておく必要がある.
実際これをもう一度微分すれば
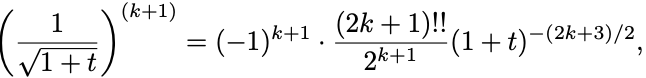
となって帰納的に示される.
よって まわりのTaylor展開は
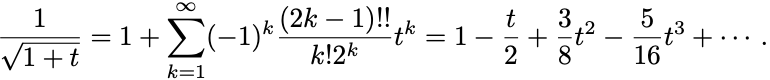
(II) は微分すると
でありもう一度微分すると元に戻る.
なので偶数冪だけが残る.
それゆえ とおいて
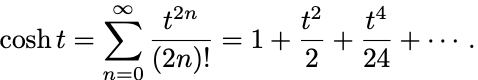
(III) (II)と同様にして は微分すると
でありもう一度微分すると元に戻る.
なので奇数冪だけが残る.
それゆえ とおいて

次の函数を まわりでTaylor展開して3次近似まで求めよ:

(I) 3階微分までを計算してみると
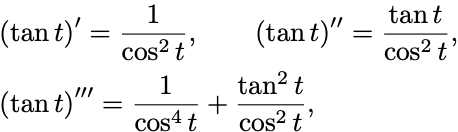
これらから
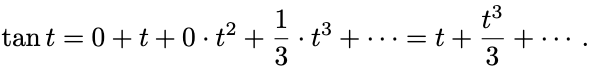
(II) 3階微分までを計算してみると
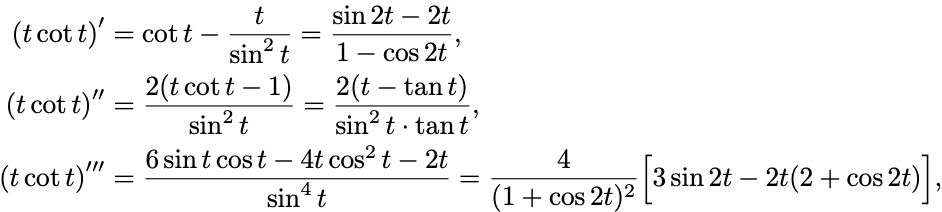
これらの での値を調べるにはl’Hospitalの定理を適用して
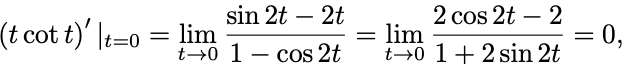
とすればよい.
2階微分では
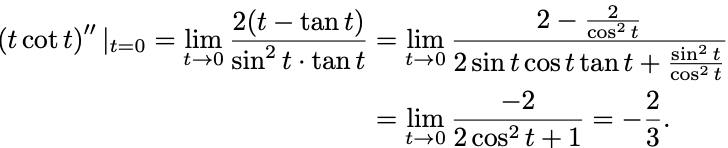
3階微分の途中計算は省略するが同じような変形を繰り返すことで
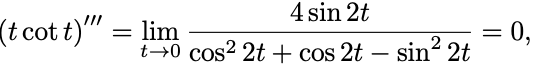
がわかる.
以上より
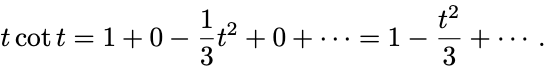
次の函数を まわりでTaylor展開せよ:
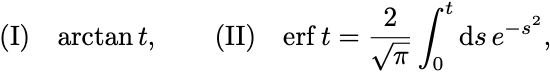
(I) のTaylor展開を求めるために函数
のTaylor展開を利用する:
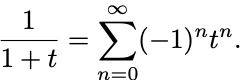
を1階微分すると
の函数として
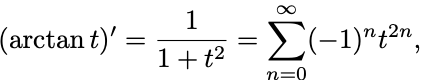
が成立する.
一方で とTaylor展開されたとすると
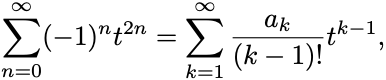
が成り立つ.
左辺には の偶数冪しか現れないから右辺で
とおいて
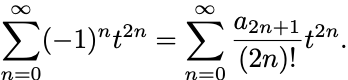
各 の冪で係数を比較して
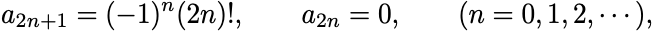
と定まる.
したがって
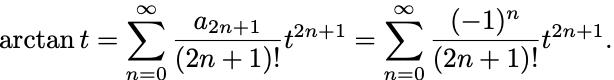
(II) のTaylor展開を求めるために函数
のTaylor展開を利用する:
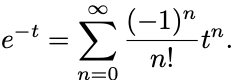
を1階微分すると
の函数として
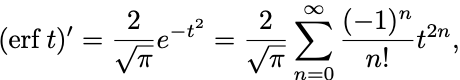
が成立する.
一方で とTaylor展開されたとすると
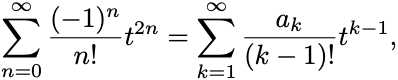
が成り立つ.
左辺には の偶数冪しか現れないから右辺で
とおいて
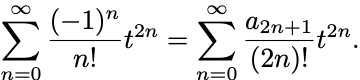
各 の冪で係数を比較して
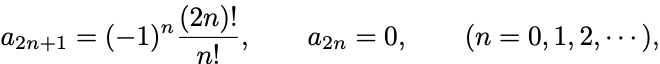
と定まる.
したがって