エントロピー最大の原理

Prerequisite

エントロピー増大の法則

この章では熱力学の再構築を議論する．
Newton力学がLagrange形式や正準形式といった洗練された形に再構築されたように，熱力学もシンプルに数個の基本原理に集約することを目指したい．
こうした試みはいくつもあり，どれが熱力学の本質かについて最先端で議論されている．
また解析力学が量子力学や統計力学の足掛かりとなるように，熱力学の再構築によって非平衡系や相対論への拡張ができないかが期待される．
たとえば非平衡定常状態の熱力学やブラックホールの熱力学はそれにあたるだろう．

この節ではエントロピー最大の原理を基本軸に熱力学を構築する．
以下を仮定しよう：

1. 任意の孤立系では，十分時間が経つと全ての熱力学変数が一定となる熱平衡状態に達する

2. 相加変数 $U,\,X_1,\cdots,\,X_n$ の函数として熱力学変数 $S=S(U,X_1,\cdots,X_n)$ が存在する．
これをエントロピーという．

3. エントロピーは内部エネルギー $U$ の単調増加函数である．

4. 部分系からなる系の熱平衡状態ではエントロピー最大の原理によって決まる：

ここで

仮定1は熱力学第〇法則であり，仮定4がエントロピー最大の原理である．

これら仮定に加えて種々の熱力学の用語などを定義しておく．
特に熱力学第一法則

によって熱 $Q$ を定義する．

仮定4を補足しておく．
最大値を探すとき，系の示量変数 $U^{(\mathrm{tot})},\,X^{(\mathrm{tot})}_1,\cdots\,X^{(\mathrm{tot})}_n$ は一定という拘束条件が課される．各部分系が熱だけを透過する壁で隔絶される場合， $U^{(\mathrm{tot})}=\sum_{\alpha}U^{(\alpha)}$ の拘束条件のもとで $U^{(\alpha)}$ をいろいろ動かした中でエントロピーは最大となる．
もし壁が断熱だが可動の場合は体積 $V^{(\mathrm{tot})}=\sum_{\alpha}V^{(\alpha)}$ の拘束条件のものとで $V^{(\alpha)}$ をいろいろ動かした中でエントロピーは最大となる．
透熱かつ可動なら両方の拘束条件のもとで $U^{(\alpha)},\,V^{(\alpha)}$ を動かした中での最大値をとる．

いま $U^{(\alpha)},X^{(\alpha)}_1,\cdots,X^{(\alpha)}_n$ を系のエントロピーを最大にする示量変数の組みとする，すなわち各部分系が平衡状態にあるとすると

が成立する．
これはエントロピーの相加性を示している．

エントロピーの相加性から凸函数であることが導かれる．
$0<\lambda<1$ を任意に選んで $\lambda U^{(1)},\,\lambda X^{(1)}_1,\cdots,\,\lambda X^{(1)}_n$ の部分系 $1$ と $(1-\lambda) U^{(1)},\,(1-\lambda) X^{(2)}_1,\cdots,\,(1-\lambda) X^{(2)}_n$ の部分系 $2$ の間の平衡状態を考える．
エントロピー最大の原理から

という不等式が成り立つ．
2つの部分系が同じエントロピーの函数形 $S^{(\mathrm{tot})}=S^{(1)}=S^{(2)}=S$ （等号は函数としての等号）の場合この不等式は

となり，ゆえにエントロピーは上に凸な函数であることが示される．
凸函数なのでLegendre変換による議論が可能となる（Helmholtzの自由エネルギー，エンタルピー，Gibbsの自由エネルギーを参照せよ）．

各示量変数に共役な示強変数を

で定義する．
$T$ は系の温度である．
ただし $U,\overline{X_i}$ は微分する際に $X_i$ 以外の変数と $U$ を固定することを意味する．
エントロピーが上に凸であることから $1/T$ と $B_i$ は単調減少函数である．
特に温度については仮定3から

の単調増加函数でなければならない．

エントロピーの微分形式はこれらの変数を用いて

と書ける．
ここで $B_0=1/T,\,X_0=U$ とおいた．
内部エネルギーについて書き換えて

とする．
ここで $Y_i:=-TB_i$ とおいた．
これらの微分形式が常に成り立つような熱力学的過程を準静的過程といい $\gamma:\mathcal{A}\overset{\mathrm{q}}{\to}\mathcal{B}$ とかく．
示量変数の変化によって系になされる仕事は $W(\mathcal{A}\overset{\mathrm{q}}{\to}\mathcal{B})=\int_{\gamma}\sum_iY_i\mathrm{d} X_i$ なので，熱力学第一法則から

とかける．
あるいは微小な準静的過程でやりとりする熱を $d'Q$ とおくと

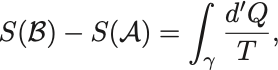
と書くこともできる．
この表式から明らかに準静的な断熱過程ではエントロピーは不変とわかる．

2つの部分系が平衡状態にあるときエントロピー最大の原理により $\delta S^{(tot)}=0$ である．
これは2つの部分系の間でやりとりのある示量変数 $X_{\lambda}$ （ $\lambda\in\Lambda$ ）を仮想的に動かしたときの最大値である．
したがって

と展開できる．
拘束条件 $X^{(tot)}_{\lambda}=X^{(1)}_{\lambda}+X^{(2)}_{\lambda}=\mathrm{const.}$ より $\delta X^{(2)}_{\lambda}=-\delta X^{(1)}_{\lambda}$ ．
したがって

なので

が導かれる（具体的な計算は部分系の熱平衡を参照）．

エントロピー最大の原理の拘束条件は部分系どうしの間の壁がどのようなものかを反映している．
それぞれの部分系が完全に隔絶されている場合より，示量変数のやりとりがある場合の方が変数の動ける範囲が広がって最大値もより大きいものを探すことができる．
すなわち壁を取り替えて部分系どうしでやりとりできる示量変数を増やすたびに系全体のエントロピーは増加する．
これを広義のエントロピーの増大則とよぶ．
反対に特定の示量変数をやりとりしない壁に戻してもそれ以上平衡状態は変化せずエントロピーは一定のままである．

着目する系と環境が断熱壁で接触している系を考える．
壁を可動壁や粒子を透過する壁に変えることで環境から着目系に仕事がなされて新たな平衡状態に達する．
これは着目系にとって断熱過程である．
上のことから系全体のエントロピーは増加するので $\delta S^{(\mathrm{tot})}=\delta S + \delta S^{(\mathrm{env})}\geq 0$ が成立する．
環境にとってはこの過程によって平衡状態はほとんど乱されず，準静的過程とみなせるならば $Q^{(\mathrm{env})}=\int\mathrm{d} S^{(\mathrm{env})}/T^{(\mathrm{env})}=0$ である．
環境の温度変化も無視するとエントロピーの変化は $\int\mathrm{d} S^{(\mathrm{env})}=\delta S^{(\mathrm{env})}=0$ がいえる．
したがって着目系のエントロピーの変化について，