Prerequisite
この節では本義Lorentz変換の群 のLie代数を調べる.
微小Lorentz変換を とおく.任意の反変ベクトル(の成分)は
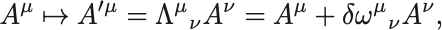
と変換する.
回転群 と同様に微小Lorentz変換は
の形にかけ,任意のLorentz変換はこの微小変換を繰り返す(積分
)ことで得られる.
の条件から
の添字を下げたものは反対称,
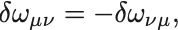
である. そのものは反対称ではないことに注意せよ.
一般に反対称テンソルは対角成分が全て であり,よって
成分のうち独立な成分は
つだけである.
そこで に
個のパラメータを導入して
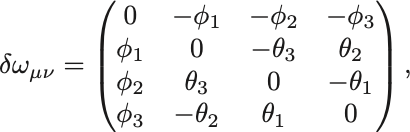
とおく.添字を上げて を計算すると
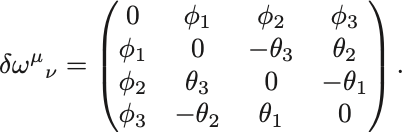
さらに 個の行列を導入して
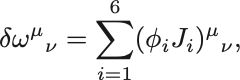
と分解する. ここで であり,
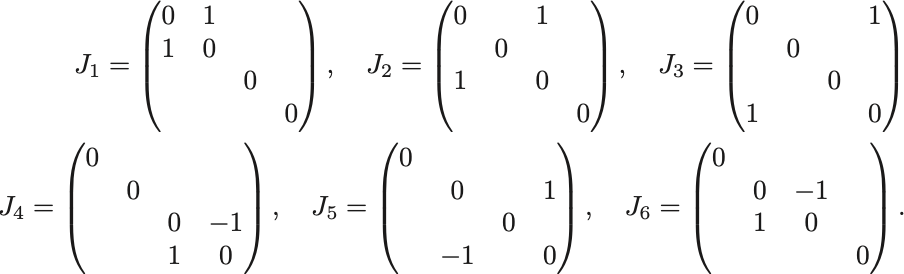
たちはLorentz群
の生成子である.
の時間成分を除けば
の生成子と一致し三次元の回転に対応していることがわかる.
たしかに三次元の回転は世界間隔を不変にするLorentz変換である.
はLorentzブーストに対応していると予想される.
に対してそのことを確かめてみよう.
から生成されるLorentz変換を
とおく.
まず を対角化する行列
を求めることから始める.
固有値方程式 より固有値は
と求まる.
それぞれに対して大きさ で規格化した固有ベクトルは
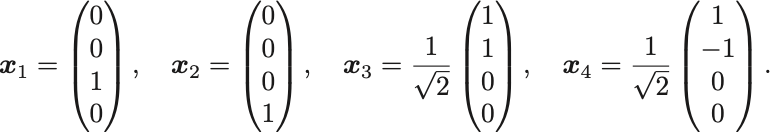
したがってこれらを並べた によって
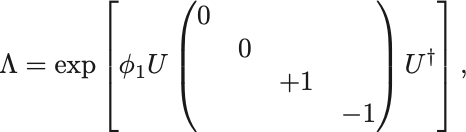
と対角化できる.
指数行列の定義 と
より
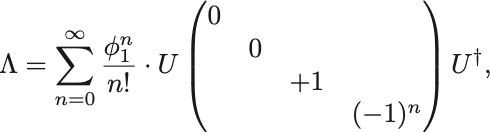
の具体形を代入して計算し,初項が
であることに注意して無限級数を各成分で整理すると双曲線函数が現れて,
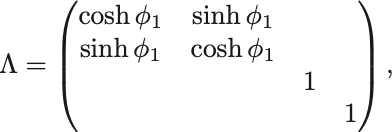
これは 軸方向の速さ
のLorentzブーストの式である.
に対しても同様の議論から
軸方向のブーストが得られる.
生成パラメータ はラピディティ (rapidity) と呼ばれる.
3次元の回転のときは回転を3つの要素, 平面内の回転に分けた.
同様に4次元では の6つに分けることができる.
軸を含む3つはその空間方向へのブーストを表し,後の3つはその平面内の回転を意味する.
よりLoretz共変性が明らかなように生成子を書き換えたい.
そこでパラメータを成分に保つ反対称テンソル を導入し,6つの生成子もテンソル表記にして
とおくと,
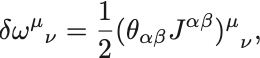
と展開する. こうおけるためには,
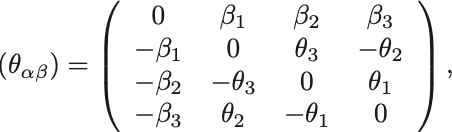
かつ,

と定義する必要がある.
註)通例は虚数 を前に出して定義するが,ここではあえてそうする理由がないので定義から省いている. 量子力学でLie代数を扱うときに定義を改める.
実際,各 について計算すればもとのLoretz変換の形に一致していることがわかるだろう.
が反対称なことから,たとえば
方向のブーストを調べたいときは
だけでなく
も計算に入ってくる.
この事情のために が前にかかっている.
たとえば である.
任意のLorentz変換は,
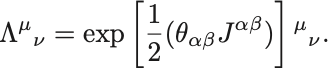
生成子 の交換関係を調べてみよう.
容易な計算から,
Lorentz代数

という関係を満たすことがわかる(Problem参照).
これをLorentz代数という.
生成子を回転とブーストに分けてその交換関係を求める.
回転は ,ブーストは
で生成される.
Lorentz代数を用いた容易な計算から以下の交換関係が導かれる:
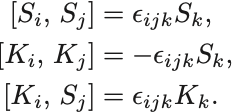
回転の生成子 たちの代数はそれらで閉じているがブーストの生成子は閉じていない.
Lorentz代数はさらに2つの 代数に分離することができる.
2つの回転に対する表現論から可能なLorentz代数の表現を2つの整数または半整数によって指定して分類できる.
詳細については場の理論の章にて述べる.
Problem
Lorentz代数を計算により確かめよ.
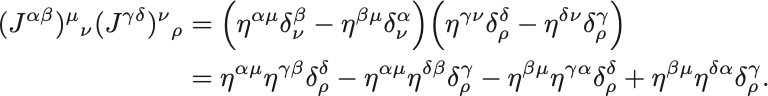
よって交換関係は,
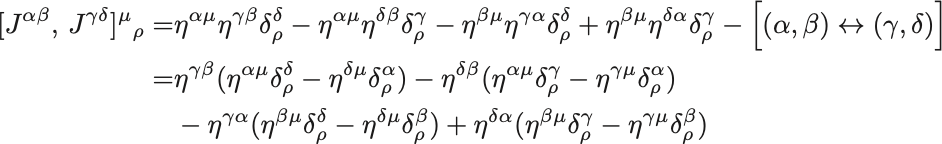
と整理できる. 括弧の中は生成子であるから添え字に注意して

を得る.