van der Waals気体

Prerequisite

• 理想気体の熱力学

ここまで理想気体をたびたび扱ってきたが理想気体の状態方程式や内部エネルギーの式，

はある条件のもとでのみ成立する近似式であった（ は気体分子の自由度に依存した定数， はBoltzmann定数）．
この節ではより実際の気体に近づけたモデルの1つであるvan der Waalsモデルを紹介する．

理想気体の近似が良いのは，気体分子間に働く引力を無視できる場合であった．
たとえば気体の密度が十分低く分子間が十分離れているときや，温度が十分高く分子の運動エネルギーが分子間引力に比べて十分大きいときなどが当てはまる．
それゆえ気体をより正確に記述したい場合には引力の効果を適切に取り入れる必要がある．
そのミクロからの導出は統計力学に委ねることにして，理想気体の状態方程式に対し修正を以下のように加える：

van der Waals状態方程式

これをvan der Waals状態方程式といい，この状態方程式に従う気体をvan der Waals気体とよぶ．

van der Waals気体の各種熱力学量を求めていこう．
まず状態方程式を圧力について解くと

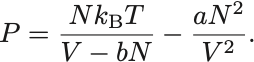
van der Waals状態方程式に現れる正のパラメータ は分子間引力に関係しており， は分子の大きさに関する量である．
密度 が非常に小さいときこれらパラメータを含む項は無視できて

となって理想気体の圧力の式に近づく．
圧力が の函数でかけていることからHelmholtzの自由エネルギーを用いて

と書けることを利用する．
この両辺を積分して

がわかる．
ここで は体積によらない函数．
を定めるためにこの自由エネルギーが密度の小さい極限で理想気体の自由エネルギー

に近づかなければならないことを課す．
体積 が非常に大きい場合，密度は小さいが はそのままなので

と近似できる．2式を比較して

と定められる．
したがってvan der Waals気体の自由エネルギーは

となる．

エントロピーは自由エネルギーの温度微分で計算できて

ただし とおいた．

次に内部エネルギーを計算しよう．
そのためには

の関係を利用すればよい．
容易な計算から

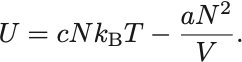
van der Waals気体の内部エネルギーには分子間引力のエネルギーの項が現れてくる．
さらに を固定した温度微分により定積比熱を計算すると

となり理想気体と同じく温度・体積に依存しない一定値である．

van der Waals状態方程式にもとづく気体のモデルは単に実在の気体に近いというだけでなく，液体への凝縮（気液相転移）を記述するという点で重要である．
詳細は相転移の章にて論じる．

Next

• Joule–Thomson過程