Newton方程式では力学的平衡な質点の運動は静止または等速直線運動となる(慣性の法則).
剛体の場合には一般にどのような運動が見られるのだろうか.
剛体の力学的平衡条件は,

である.
それゆえ剛体の重心の運動は静止または等速直線運動することがただちにわかる.
次に重心回りの回転運動について見ていこう.
慣性主軸 をとり,そこから見たEuler方程式は,
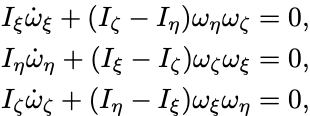
となる.
3つの方程式を一般に解析することは困難なので,慣性モーメントが特別な場合に注目して議論する.
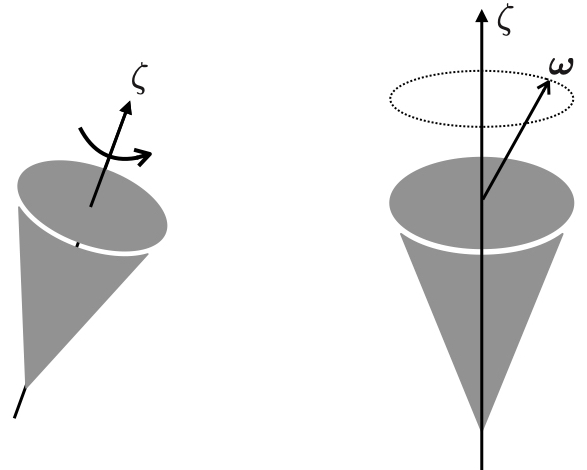
1つ目の例として主慣性モーメントが軸対称, の場合を考える.
このような剛体を対称コマ (symmetric top),あるいはLagrangeコマとよぶ.
このときEuler方程式の 成分は
となるので,
ならば,
である.
残りの方程式は,

となる.ここで,
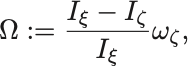
とおいた.
1つ目の方程式の両辺をもう一度時間微分して,2つ目の方程式を代入して を消去すれば,
に関する方程式,
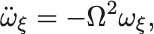
を得ることができる.
この方程式は角振動数 ,周期
の単振動を表す.
一般解は となる.
この一般解を1つ目の方程式に代入することで もわかる.
以上から対称コマの角速度ベクトルは 軸方向には一定で,
平面内を円運動することがわかった.
このような角速度ベクトルのふるまいは歳差運動 (precession) とよばれる.
角運動量ベクトルは なので同様に歳差運動する.
ただし一般に と
は平行ではないことに注意せよ.
2つ目の例として1つの慣性主軸周りにだけ回転する場合を考えよう.
このとき他の軸まわりの回転については小さい影響だけ考慮する.
主慣性モーメントの大小関係を としても一般性を失わない.
Euler方程式を3つの軸それぞれで回転する場合について議論する.
まず 軸周りの回転
を考える.
すると1つ目の方程式から が成り立ち,ゆえに
は定数とみなせる.
残りの方程式は,

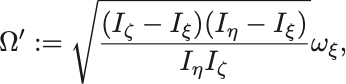
となり, は単振動する.
軸回りの回転
も同様に議論できて,
が定数,
が単振動となる.
問題は 軸回りの回転,
の場合である.
同様の近似で となる.
残りの方程式は,

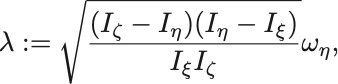
となる.
方程式の符号に注目するとこれは単振動を表さないことに気づく.
あえて とおくとみかけは単振動と同じになるので,単振動の一般解を適用して,
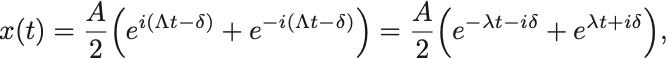
となる.
右辺の第2項に注目すると,因子 は時間とともに指数函数的に増大する.
これは最初の摂動の仮定に反する.
したがって,はじめ 軸周りの回転だけを考えていたのだが,時間発展とともに他の2軸周りの回転の影響が増大していき,近似式は破綻してしまう.
このような運動は不安定であるという.
以上をまとめると剛体の3つの慣性主軸まわりの回転のうち慣性モーメントが最大,最小の場合は安定であり,中間の場合は不安定となる.
この事実をテニスラケットの定理という
註)俗にはDzhanibekov効果としても知られる.
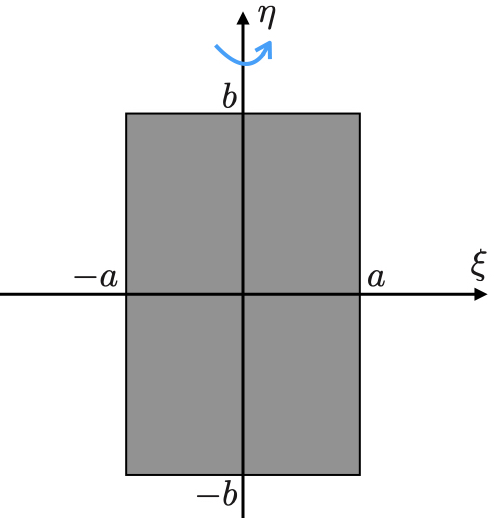
軸方向に
,
軸方向に
の長方形を例にとってみよう.
このとき慣性モーメントは であり,
の大小関係にある.
長方形はそれが含まれる面内での回転で安定であり,短い方の辺を回転軸にしたときも安定である.
ところが長い方の辺を回転軸にした場合は不安定な回転となる.