Prerequisite
この節では系は孤立していて,質点は有界な領域の中で運動するとする.
孤立系なのでエネルギーも保存し,運動量も有界である.
系のHamiltonianを とすると,位相空間の軌道は
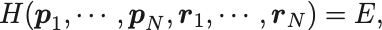
の表す超曲面上に限られる.
座標も運動量も有界なのでこの超曲面は閉曲面である.
この閉超曲面が囲む領域を とし,閉超曲面を
とおく.
このとき系の確率密度函数の規格化条件は
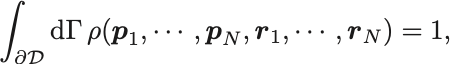
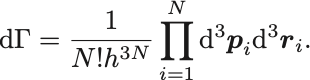
となりエントロピーは

によって計算可能である.
孤立系の確率密度に対しては次の仮定をおく:
等重率の原理
上の事象は同様に確からしい一様分布である.
これを等重率の原理 (principle of equal a priori weights) という.
これはデータに基づかない事前分布である.
等重率の原理により確率密度函数を定数函数
ミクロカノニカル分布
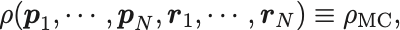
と書き下せる.
これをミクロカノニカル分布または小正準分布という.
規格化条件は
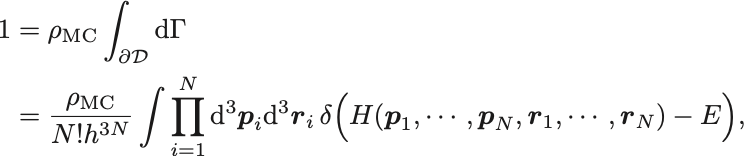
となる.ここで
状態数
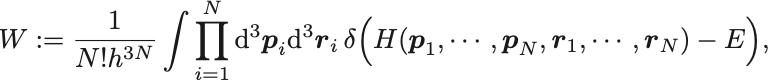
とおくと超曲面 上の状態の総数に等しい.
は系の状態数と呼ばれる.
また後ろの積分は超曲面 の面積に等しい.
状態数を用いてミクロカノニカル分布は
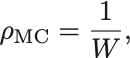
とかける.エントロピーは
Boltzmannの式

と書ける.
この式はBoltzmannの式として知られる.
状態数が大きければエントロピーも大きいので,エントロピーは系の「乱雑さ」の指標として解釈されることがある.
具体的な例でミクロカノニカル分布を求めてみよう.
最も簡単なのは相互作用しない自由な質点の系で,Hamiltonianは
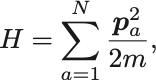
とかける. は質点の質量.
エネルギー一定の超曲面は少し変形して,
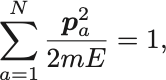
でありこれは中心原点,半径 の
次元球面を表す.
エネルギーが与えられると運動量の値はこの球面上にしか存在できない.
数学の公式から 次元の球の表面積
は,
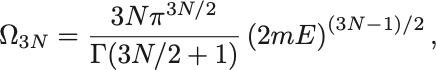
で与えられる.
座標の積分からは が得られるから,
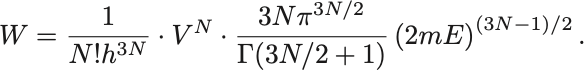
エントロピーはStirlingの公式 とガンマ函数の漸近展開を用いて,
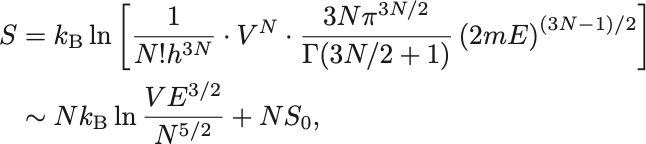
と計算される. は定数.
ここで は非常に大きいとして
などの項は無視した.
熱力学では内部エネルギー を用いるが孤立系では
である.
したがってエントロピーが の函数として

と求められる.
これは理想気体のエントロピーの式である.
温度の定義により

よって
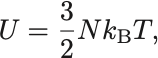
が導かれる.
また示強変数としての圧力の定義により

よって
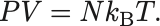
これは理想気体の状態方程式である.
上の導出でわかるように が非常に大きいために冪の
などは
で近似できる.
このことからエネルギー一定面の面積を,その閉曲面が囲む体積で近似してもよい.
たとえば半径 の
次元球面の表面積は
のオーダーに対し体積は
のオーダーである.
したがって が非常に大きいならば球の表面積を体積で近似できる.
典型性の言葉で言えば,エネルギー一定面 上の状態数に比べて,その内部の状態数は非常に少ないので標本空間を
へ拡大しても問題ないといえる.
こうして広義のミクロカノニカル分布
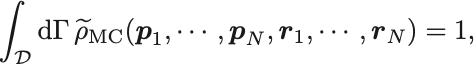
を採用することもある.
